我是安周

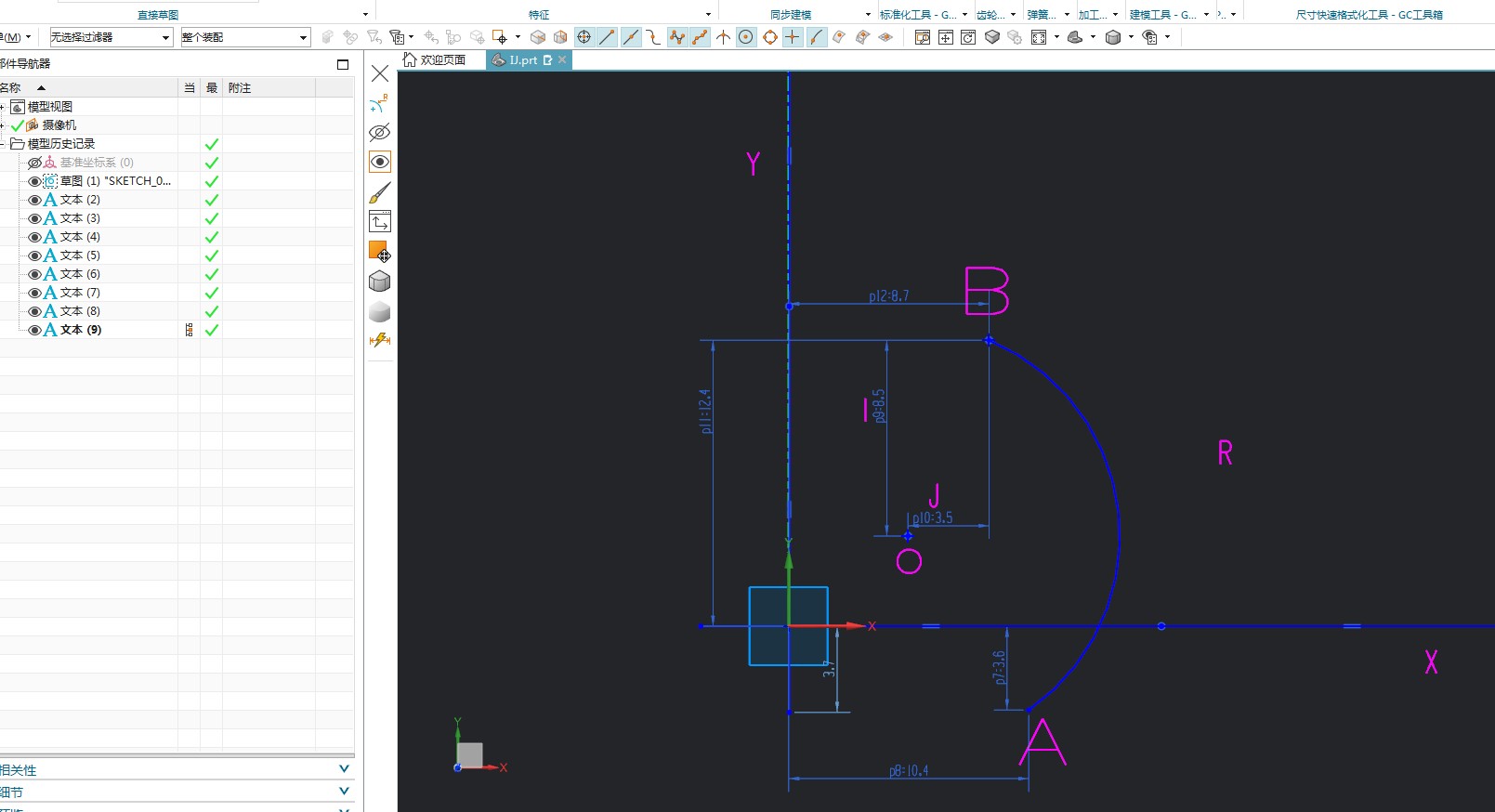
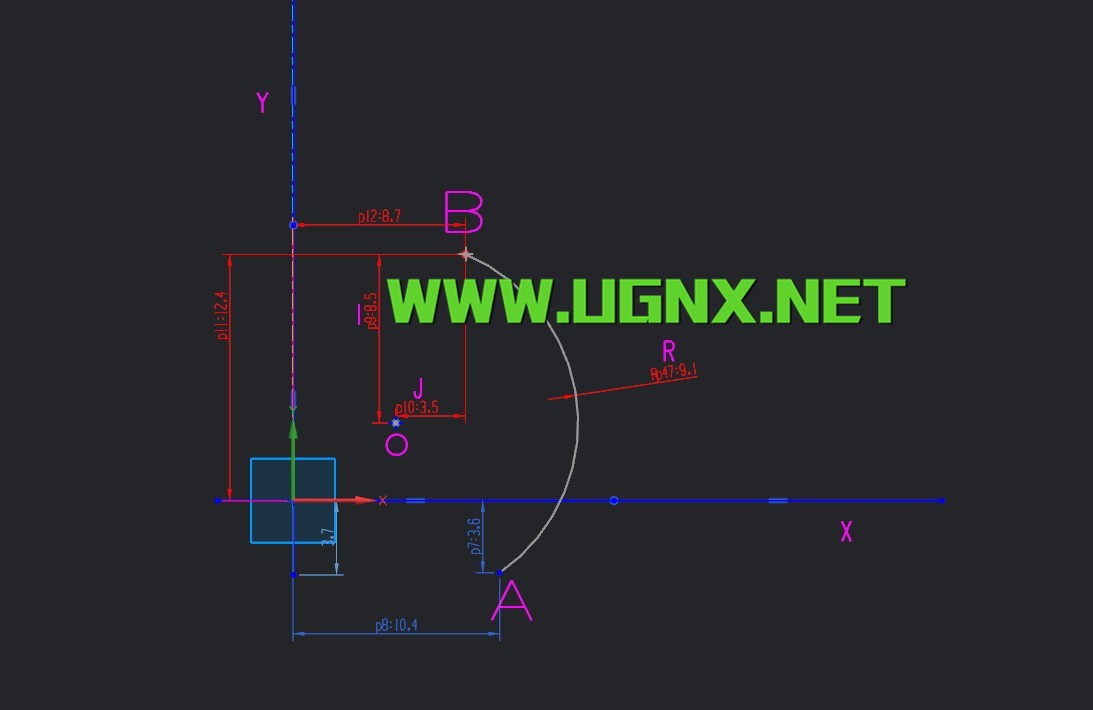
       相信每个编程和调机都遇到过机床报警圆弧误差，下来我用数学证明一下，当然有很多种办法走圆弧 ，R 或者点位坐标

I、J、K 为起点B指向圆弧中心O的向量；

I、J、K 分别对应X、Y、Z轴方向；

I、J、K 带符号，指向X、Y、Z轴正方向时为正，指向X、Y、Z轴负方向时为负。

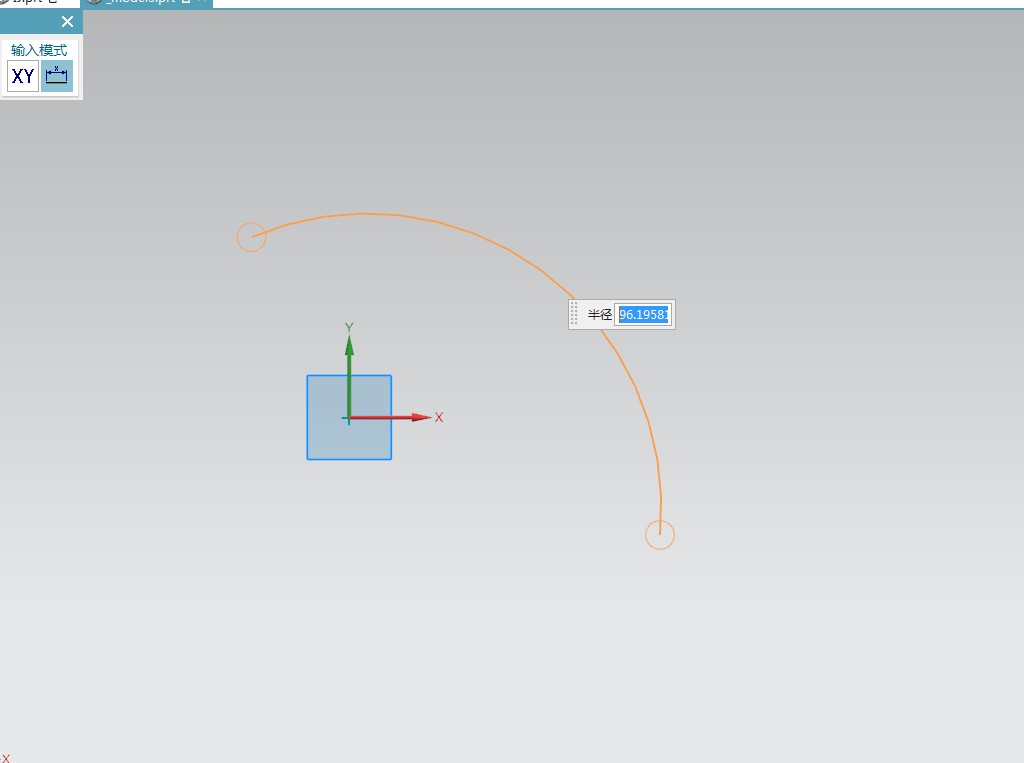
我做了一个数学模型

以半径R做点B到点A的圆弧运动

点B （P12,P11）         点BA（P8,P7）

           I (p9)                   J（p10）

从图中可以看到 OA=OB=R=√I²+J²

现在我在NX中标注一个R，因为这个R是已知的 OA=OB

现在处于过约束状态，其实机床在走IJ就是一个过约束状态（三销定位），过约束需要一定的误差，间隙，弦差，机床有一个圆弧误差参数，当超出误差值就会报警。

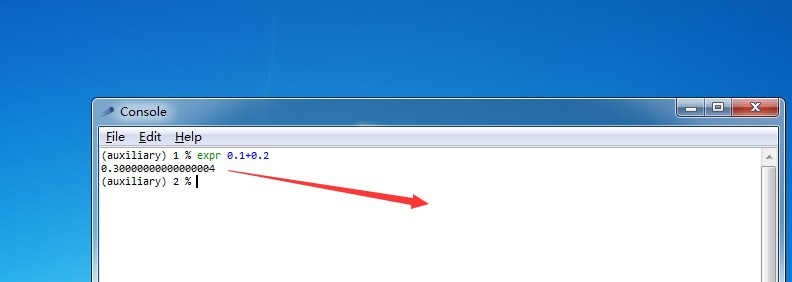
下来说说计算机浮点问题，这是导致报警直接的原因

0.1+0.2的运算

首先，要站在计算机的角度思考 0.1 + 0.2 这个看似简单的问题。能被计算机读懂的是二进制，而不是十进制，先把 0.1 和 0.2 转换成二进制看看：
0.1 => 0.0001 1001 1001 1001…（无限循环）
0.2 => 0.0011 0011 0011 0011…（无限循环）
双精度浮点数的小数部分最多支持 52 位，所以两者相加之后 0.0100110011001100110011001100110011001100110011001100 因浮点数小数位的限制而截断的二进制数字，这时候，再把它转换为十进制，就成了 0.30000000000000004。

       0.1+0.2其实不等于0.3的，只是取决于我们需要的小数位数。

   一般三轴机床用小数点2位在大多数，笔者见用过3位小数报警的机床。

 +0.0046

 -0.0046

这两个值当取小数点2位，都等于0，其实它的误差已经是0.0092

用IJ走圆弧需要一个起点（X1 Y1） 终点（X2 Y2） 圆心（X Y）  

需要6个坐标，最坏的结果就是误差累计导致的终点坐标不在圆弧轨迹上，直接导致报警，这其实是求点在轨迹上的一个运动做判断。

那么解决的办法当然很多，这里简单的介绍一个思路，需要加强一下后处理这块。

    用已知R OA OB  半径 ，起点， 终点  反求IJ   用NX提供的IJ和计算的IJ各取两位小数做判断    误差取决于机床圆弧误差，超差就取运算的值。

这里有一个技巧就是 将这些值在运算之前先升幂（X*10^n）  计算完之后再降幂（X*10^-n），0.03变为0.3或者更高  计算完不要忘记降幂，可以很好避免由于计算误差带来的小数位舍去 ！

   这个思路主要是计算机浮点带来的问题，从根本上已经解决了浮点舍去的问题。

  在这我顺便说说为什么用R不会报警，因为已知两点可以做无数条圆弧，不构成过约束，允许有误差。

在海德汉上面，走圆弧至少有4种方法  可以用极坐标走PA的形式，指定起点，指定R   指定角度  即可完成！ （当然海德汉一般最少3位小数，笔者用的4位）

在海德汉530上面PI=3.142   在640上面 PI=3.141   这个也是海德汉升级之后一个大提升。